In de eerste aflevering van Lewis (de sequel van de politieserie Morse) komt de fascinatie voor perfecte getallen aan bod. Het speelt zich dan ook af in Oxford. Perfecte getallen zijn gehele getallen die gelijk zijn aan de som van hun deelcijfers. Het kleinste perfecte getallen is 6, want deelbaar door 1 ,2 en 3 die opgeteld 6 zijn. Kunnen wij deze getallen vinden met een klein javascript? We gaan het op 2 manieren proberen.
Onze eerste poging
We gaan ervan uit dat je een html kunt maken met een extern javascript daaraan gekoppeld. Kijk anders op https://www.w3schools.com/js/js_whereto.asp voor uitleg.
In het javascript creeren we eerst een lege lijst (met de naam “lijst”) waar de perfecte getallen in kunnen komen. De tweede variabele is een getal p, wat ons gevonden perfecte getal wordt. Telkens als we er een gevonden hebben, voegen we p aan de lijst toe en maken we p weer leeg.
Het essentiële gedeelte gebeurt in een for-loop, die je uit je hoofd moet kunnen typen. We lopen door alle getallen (van 1 tot 9999) en pèr getal, checken we door welke cijfers dat getal gedeeld kan worden. Dat doen we met een tweede, geneste for-loop :
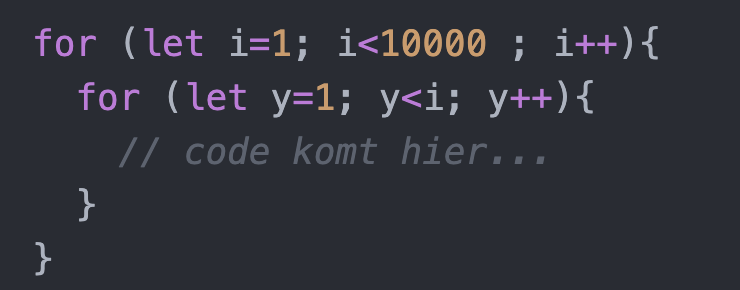
Met de modulus (de restwaarde van een deling) kunnen we zien of i gedeeld door y een geheel getal is. Als dat zo is, tellen we y bij p op:

Tot slot, checken we of p gelijk is aan i. In dat geval is p een perfect getal! En wordt p aan de lijst toegevoegd.

In onderstaand javascript zie je het eindresultaat. Er is een functie gebruikt maar dat maakt niet wezenlijk uit. We stoppen nu bij 10000, want het vijfde perfectie getal is 33.550.336, die rekenkracht kan onze browser niet aan met dit onderstaand script. Hierna voglt een tweede poging. Klik op “Result” voor het resultaat.
See the Pen Untitled by jean francois roebers (@jeanfrancoisroebers) on CodePen.
Nicomachus van Gerasa
Op de pagina van Wikipedia over perfecte getallen, staat de formule om deze te berekenen. Al rond het jaar 100 noteerde Nicomachus van Gerasa de stelling: “Als 2n-1 een priemgetal is, zijn perfecte getallen te schrijven als 2 n − 1 ( 2 n − 1 )“. Dit kunnen we nu gebruiken om het vijfde perfecte getal te vinden. We hebben in het onderstaande script een lijst gemaakt met veel priemgetallen. Voor machtsverheffen gebruiken we 2 maal **. Nu heeft de browser in heel korte tijd ook het vijfde perfecte getal gevonden.
See the Pen Vijf_perfecte_getallen by jean francois roebers (@jeanfrancoisroebers) on CodePen.
De Array met de priemgetallen is nu nog niet lang genoeg om meer perfecte getallen te vinden. Maar wacht eens, die lijst met priemgetallen hebben we helemaal niet nodig.
Een beter script: nu 8 perfecte getallen!
Hieronder staat een veel beter script waar we iedere macht van 2 (min één) checken of het een priemgetal is. Dan kunnen de stelling van Nicomachus weer toepassen. Dit script vraagt wel wat tijd (± 15 sec) maar dan we hebben de eerste acht perfecte getallen!
6
28
496
8.128
33.550.336
8.589.869.056 (meer dan 8 miljard)
137.438.691.328 (met dan 137 miljard)
2.305.843.008.139.952.000 (meer dan 2 triljoen)
See the Pen meer_perfecte_getallen by jean francois roebers (@jeanfrancoisroebers) on CodePen.
Hoe Nicomachus van Gerasa tot zijn stelling kwam is natuurlijk gissen. Hij zocht naar de mystieke en goddelijke betekenis van getallen en op zoek naar de link tussen de machten van 2, priemgetallen en perfecte getallen viel hem waarschijnlijk iets op. Laten we de machten van 2 onder elkaar zetten:
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
Als in dit rijtje het getal – 1 gelijk is aan een priemgetal, dan is de macht -1 vermenigvuldigd met de vorige macht van 2 een perfect getal. Kijk maar:
21 = 2
22 = 4 : 3 is een priemgetal. En 3 x 2 = 6
23 = 8 : 7 is een priemgetal. En 7 x 4 = 28
24 = 16
25 = 32 : 31 is een priemgetal. En 31 x 16 = 496
26 = 64
27 = 128 : 127 is een priemgetal. En 127 x 64 = 8128
28 = 256
Bijna 2000 jaar geleden heeft hij dus een verband gevonden en kon hij de eerste vier perfecte getallen vastleggen. Tegenwoordig zijn er 51 bekend. Hier zijn we al blij met de eerste acht.
Toch geen perfecte stelling
De stelling van Nicomachus is niet juist. Zo bewees in 1536 Hudalrichus Regius dat 210 (211-1) geen perfect getal is. Zie deze pagina over perfecte getallen. Waarom in het javascript dit niet blijkt is mij een raadsel… Mocht je het weten, laat me dat dan weten, bedankt!